Abbildungen
Eines der grundlegendsten Prinzipien der 3D Programmierung ist die Verwendung von Transformationen (bzw. Abbildungen).
Folgende Transformationen spielen eine Rolle:
- Modellierung
Verschiebung (Translation)
Drehung (Rotation)
Skalierung (Scale)
Spiegelung (Mirror)
- Projektion
orthogonale Projektion
perspektivische Projektion
Matrizen
Definition
Jede dieser Abbildungen wird durch eine Matrix dargestellt. Aber keine Angst! Man
muss nicht alles über Matrizen wissen. um sie anzuwenden. Wer sich genauer
informieren will, der sollte am Besten bei
Wikipedia
nachlesen. Man sollte aber
zu mindest wissen, dass eine Matrix aus 16 Zahlen besteht (4X4-Matrix). Diese Matrix kann
auf einen Vektor angewandt werden. Dies geschieht mathematisch nach ganz
bestimmten Regeln.
Für uns ist das aber nicht so wichtig. Wir müssen nur wissen, wie das zum
Programmieren funktioniert.
Nehmen wir an, wir wollen einen Körper rotieren lassen.
Eine Rotation ist bestimmt durch eine
Rotationsachse und durch einen Rotationswinkel Alfa.
Der Körper besteht aus vielen Punkten P1,P2,P3,... vom Typ xyz.
Zuanächst besorgen wir uns eine Matrix:
// Rotationsachse festlegen gegeben durch den Punkt 1,2,1
//und die Richtung 0,0,1.
LineType Rotationsachse = new LineType(new xyz(1,2,1), new xyz(0,0,1));
// Matrix besorgen
Matrix Rotation = Matrix.Rotation(Roationsachse,Alfa);
Nun rotieren wir die Punkte
P1 = Rotation*P1;
P2 = Rotation*P2;
P3 = Rotation*P3;
//usw.
Ist doch gar nicht so schwer :)
Wie kommt man zu den Matrizen?
- Modellierungsmatrizen
Translation
: Matrix Trans =
Matrix.Translation(xKoordinate,yKoordinate,zKoordinate).
Rotation: Matrix Rot = Matrix.Rotation(Drehgerade,Drehwinkel).
Skalierung: Matrix Skal = Matrix.Scale(xFaktor, yFaktor, zFaktor) .
Spiegelung: Matirx Spigel = Matrix.Mirror(Ebenes).
- Projektionsmatrizen
Orthogonale Projektion
: Matrix NormalProjection =
Matrix.Orthogonal(Left, Right,Bottom, Top, Near, Far).
Perspektivische Projektion: Matrix Perspektive =
Matrix.Frustum(Left, Right,Bottom, Top, Near, Far).
Für die Bedeutung der Parameter stelle dir sich am Besten vor: Du steht vor dem
Fenster und schaut hinaus in die weite Welt. "Left" ist der Abstand zum
linken Rand des Fensters und "Right" zum rechten Rand; ebenso stellst du dir
"Bottom" und "Top" vor.
"Near" ist der Abstand zum Fenster und "Far" ist eine Distanz, ab welcher du
nichts mehr siehst (oder sehen magst). Die Graphikengine clippt alles außerhalb des Bereiches "Left",
"Right"; "Bottom", "Top"; "Near, "Far".
Abbildungen verknüpfen
Oft sind Abbildungen nicht reine Drehungen oder Translationen sondern
"Überlagerungen". Man kann zuerst etwas Verschieben und dann Drehen.
Beide
Abbildungen zusammen ergeben eine neue Abbildung. Sagen wir zu ihr "DrehTrans".
Ist D die Matrix der Drehung und T die Matrix der Verschiebung, so bekommt man
die Matrix von "Drehtrans" durch eine
sog. Matrixmultiplikation D*T.
Dieser
Multiplikation liegt ein ganz bestimmtes
Schema zu Grunde.
Ich möchte dich aber nicht quälen mit einer langen Abhandlung darüber.
Wichtig ist, dass es ein Unterschied ist, ob zuerst verschoben und dann gedreht
wird oder umgekehrt.
Beispiel: Verschieben wir einen Körper in Nullpunktslage um einen Vektor (1,0,0) und
drehen ihn dann um den Nullpunkt mit 45°.
Das Ergebnis: Der Köper befindet sich an der Stelle (1,0,0) und ist dort um 45°
gedreht.
Umgekehrt: Drehen wir den Köprer um 45° und verschieben ihn dann um (1,0,0).
Das Ergebnis: Der Körper ist gedreht, liegt aber auf der Geraden, die mit der
x-Achse 45° einschließt ( der Mediane )!
Die Matrizenmultiplikation ist also
nicht vertauschbar.
Die Modellmatrix und die Projektionsmatrix einer Grafikengine
Eine Grafikkarte hat zwei Transformationen eingebaut:
-
Modellmatrix
-
Projektionsmatrix
Gibt man einen Punkt Pt an die Grafikkarte, so wird zuerst die
Modellmatrix M angewandt und anschließend die
Projektionsmatrix P:
Pt --> M*Pt --> PT*M*Pt
Liegt das Ergebnis innerhalb des Wüfels [-1,1]X[-1,1]X[-1,1] so hat der Punkt Glück und wird gezeichnet.
Beispiel
Es wird Zeit, dass wir wieder einmal mit einem Programm anschauen, wie das alles funktioniert.
Erstellen wir ein Drawing 3d Projekt wie es in
Hello World beschrieben ist und
nennen es "Transformations 3D".
Wir zeichnen eine Szene bestehend aus vier Würfeln:
public override void OnPaint()
{
base.OnPaint();
drawBox(new xyz(-2, -2, 0), new xyz(2, 2, 2));
drawBox(new xyz(-2, 2, 0), new xyz(2, 2, 2));
drawBox(new xyz(2, 2, 0), new xyz(2, 2, 2));
drawBox(new xyz(2, -2, 0), new xyz(2, 2, 2));
}
Und so sieht es aus
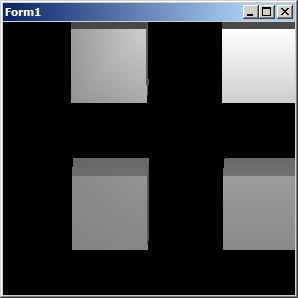
Wir drehen nun die Szene um 45° um den Nullpunkt und setzen dazu in der Paintmethode die Modelmatrix auf
die Rotationsmatrix Rot:
public override void OnPaint()
{
base.OnPaint();
Matrix Rot = Matrix.Rotation(new LineType(new xyz(0, 0, 0), new xyz(0, 0, 1)), System.Math.PI / 8);
Device.ModelMatrix = Rot;
drawBox(new xyz(-2, -2, 0), new xyz(2, 2, 2));
drawBox(new xyz(-2, 2, 0), new xyz(2, 2, 2));
drawBox(new xyz(2, 2, 0), new xyz(2, 2, 2));
drawBox(new xyz(2, -2, 0), new xyz(2, 2, 2));
}
Und sehen die gedrehte Szene

PushMatrix PopMatrix und MulMatrix
Im vorigen Beispiel haben wir einfach
...
ModelMatrix = Rot;
...
gesetzt. Dabei geht der Inhalt der ModelMatrix verloren. Um dies zu vermeiden
gibt es eine elegante Lösung, die auch von der Grafikkarte unterstützt wird.
Mit PushMatrix kann eine Matrix auf einen Spael gelegt werden mit PopMatrix
wieder aktiviert werden.
...
PushMatrix();
ModelMatrix = Rot;
PopMatrix();
...
Ein weiterer Schönheitsfehler: Bei der Darstellung einer Szene sind die Transformationen
meistens relativ zur augenblicklichen Transformation. Um eine relative Transformation auszuüben,
verwendet man
MulMatrix. Auch diese Operation ist sehr schnell, da sie von der Grafikkarte
unterstützt wird.
Also
...
PushMatrix();
ModelMatrix = Rot;
PopMatrix();
...
Ein Beispiel
...
Matrix Verschieben = Matrix.Translation(3,0,0);
PushMatrix();
DrawBox(new xyz(2,2,2));
MulMatrix(Verschieben);
DrawBox(new xyz(2,2,2);
MulMatrix(Verschieben);
DrawBox(new xyz(2,2,2));
MulMatrix(Verschieben);
DrawBox(new xyz(2,2,2));
PopMatrix();
...
Es werden vier Würfel im Abstand 3 gezeichnet und am Schluss wird der ursprüngliche Inhalt
der Modelmatrix wieder hergestellt.